Two novel symmetric multidimensional affine nested variations of the Hill Cipher are presented. The Hill Cipher is a block polygraphic substitution encryption scheme based on a linear transformation of plaintext characters into ciphertext characters. In the time since Hill first published his encryption scheme, variations, modifications, and improvements of theoretical and practical importance have been published every year indicating that the Hill Cipher is an active area of cryptography research. The first variation presented in this paper incorporated invertible key matrices of orders 2, 4, and 8 such that the matrix values of the 2×2 matrix rotate positions with each block of characters in a similar manner to the rotating letter wheels of a German Enigma Encoder, then results of the 2×2 key matrices output are passed to 4×4 key matrices, and 8x8 key matrix, 4×4 key matrices, and rotative-value 2×2 key matrices. The second variation is configured with invertible key matrices of orders 4, 8, and 16 without rotation of matrix values in a similar manner to the first variation. In both variations, plaintext characters of each block are operated on by exclusive-or (XOR) vectors prior to multiplication with the matrices to create the affine ciphers. Strengths, weaknesses, and other considerations are provided in the discussion. Two proposals are also argued with rationale for a more robust character set for encryption and the increase in modulus that the character set allows, and the possible advantages and disadvantages of affine XOR vectors.
| Published in | Mathematics and Computer Science (Volume 9, Issue 3) |
| DOI | 10.11648/j.mcs.20240903.11 |
| Page(s) | 46-56 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Cryptography, Hill Cipher, Matrix Theory, Invertible Matrices
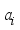 is the affine element component as:
is the affine element component as: 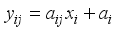 over a field.
over a field. Object | Dimension | Number Required |
|---|---|---|
Pseudo-Key XOR Row Vector | 1x2 | 12 |
Pseudo-Key XOR Row Vector | 1x4 | 2 |
Pseudo-Key XOR Row Vector | 1x8 | 3 |
Key Matrix | 2x2 | 8 |
Key Matrix | 4x4 | 4 |
Key Matrix | 8x8 | 1 |
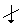 symbol normally represents an input (down-arrow) and the number of bits (to the right of the forward slash /). However, the Hill Cipher literature traditionally represents alphabet characters as both input and output, rather than a number of bits. Following this practice, and in slight abuse of the bit-use in conventional encryption-decryption diagrams, the number represented in Figure 2 in the upper right of the forward slash / will represent the number of alphabet characters that will input in the direction of the down-arrows rather than the number of bits.
symbol normally represents an input (down-arrow) and the number of bits (to the right of the forward slash /). However, the Hill Cipher literature traditionally represents alphabet characters as both input and output, rather than a number of bits. Following this practice, and in slight abuse of the bit-use in conventional encryption-decryption diagrams, the number represented in Figure 2 in the upper right of the forward slash / will represent the number of alphabet characters that will input in the direction of the down-arrows rather than the number of bits. 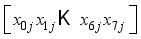 for characters
for characters 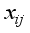 (
( 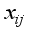 : ith element of the jth block) where i is the character number and j is the block.
: ith element of the jth block) where i is the character number and j is the block. 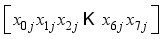 XOR
XOR 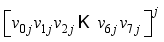 modulo p, where
modulo p, where 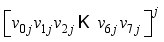 is interpreted as
is interpreted as 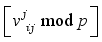 for i = 0 to 7.
for i = 0 to 7. 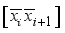 , in Figure 2) to xor in step 4.
, in Figure 2) to xor in step 4. 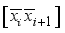 in the above step with the jth power each of one of the 4 random 1x2 pseudo-key xor row vectors respectively.
in the above step with the jth power each of one of the 4 random 1x2 pseudo-key xor row vectors respectively. 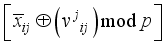 for i = 0, 3 in Figure 2.
for i = 0, 3 in Figure 2. 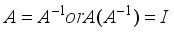 where I is the identity matrix, and by inspection that the matrix is not circulant.
where I is the identity matrix, and by inspection that the matrix is not circulant. 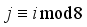 , Table 2, in a similar manner to rotor wheels in German Enigma Encoders shown in Figures 3 and 4.
, Table 2, in a similar manner to rotor wheels in German Enigma Encoders shown in Figures 3 and 4. 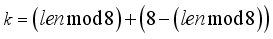 using appropriate padding.
using appropriate padding. 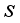 of all 8 matrices of order 2 with respect to the jth block will allow tracking necessary for decryption where the block j=0 is the initial state of the matrices with respect to the original orientation of their matrix values. Since there is a one-to-one correspondence between plaintext and ciphertext characters, the length can be determined, and from the length, the state of all order 2 matrices can be calculated in a similar manner to an established protocol
of all 8 matrices of order 2 with respect to the jth block will allow tracking necessary for decryption where the block j=0 is the initial state of the matrices with respect to the original orientation of their matrix values. Since there is a one-to-one correspondence between plaintext and ciphertext characters, the length can be determined, and from the length, the state of all order 2 matrices can be calculated in a similar manner to an established protocol 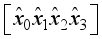 and
and 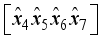 .
. 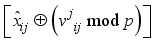 for i = 0, 1 in Figure 2.
for i = 0, 1 in Figure 2. 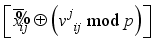 for i = 4, 7 in Figure 2.
for i = 4, 7 in Figure 2.  with respect to the jth block will allow tracking necessary for decryption where the block j=0 is the initial state of the matrices with respect to the original orientation of their matrix values.
with respect to the jth block will allow tracking necessary for decryption where the block j=0 is the initial state of the matrices with respect to the original orientation of their matrix values. 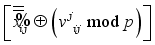 for i = 8, 11 in Figure 2.
for i = 8, 11 in Figure 2. 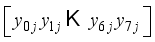 representing the jth block of plaintext
representing the jth block of plaintext 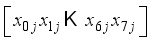 .
. 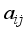 for i,j = 1 to 2:
for i,j = 1 to 2: 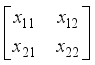 . Let the matrix value
. Let the matrix value 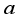 in the 2x2 rotor matrices be rotated as clockwise one-quarter turn in Step 5 with respect to Figure 2 as further explained below. For ease of visualization, the matrix values are noted in alphabetical order. The convention will be to rotate the values of the 2x2 matrices for each block j
in the 2x2 rotor matrices be rotated as clockwise one-quarter turn in Step 5 with respect to Figure 2 as further explained below. For ease of visualization, the matrix values are noted in alphabetical order. The convention will be to rotate the values of the 2x2 matrices for each block j 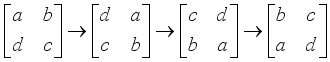 . The initial value positions will be the assignment
. The initial value positions will be the assignment 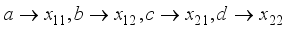 . The state can now be stated as in Table 2 with respect to the plaintext length, assigned matrix number i, and the jth block. For example, with a plaintext character length of 8, and the 0th block, the matrix values are in the initial state. Matrix values will rotate clockwise one-quarter turn such that the matrix values will now be
. The state can now be stated as in Table 2 with respect to the plaintext length, assigned matrix number i, and the jth block. For example, with a plaintext character length of 8, and the 0th block, the matrix values are in the initial state. Matrix values will rotate clockwise one-quarter turn such that the matrix values will now be 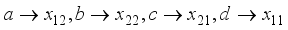 as
as 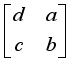 . Rotate clockwise one-quarter turn the matrix
. Rotate clockwise one-quarter turn the matrix 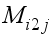 (
( 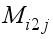 : ith 2x2 Matrix, jth block) when
: ith 2x2 Matrix, jth block) when 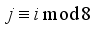 . Initialize
. Initialize 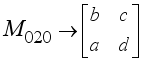 prior to passing the first block j = 0 through the encryption process. Once the plaintext character length is known, which also means the ciphertext character length is known, the number of 8-character blocks j is known. By the rotation scheme above, it is deterministic to configure each of the eight 2x2 matrices in the correct orientation for decryption. Hence, the block number corresponds to which 2x2 matrices have rotated and taking the block number mod 8 indicates how many times the particular 2x2 matrix has rotated, which indicates which state the particular 2x2 matrix is in according to Table 2. The integer portion of
prior to passing the first block j = 0 through the encryption process. Once the plaintext character length is known, which also means the ciphertext character length is known, the number of 8-character blocks j is known. By the rotation scheme above, it is deterministic to configure each of the eight 2x2 matrices in the correct orientation for decryption. Hence, the block number corresponds to which 2x2 matrices have rotated and taking the block number mod 8 indicates how many times the particular 2x2 matrix has rotated, which indicates which state the particular 2x2 matrix is in according to Table 2. The integer portion of 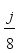 represents the number of times all matrices have rotated. When the block number j is a multiple of 8, all of the 2x2 matrices are in State 0. State configuration for 2x2 rotor Matrix
represents the number of times all matrices have rotated. When the block number j is a multiple of 8, all of the 2x2 matrices are in State 0. State configuration for 2x2 rotor Matrix 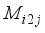 is
is 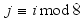 .
. State 0 | State 1 | State 2 | State 3 |
|---|---|---|---|
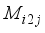 for
for 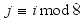
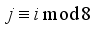 . The ciphertext length, len, is known which also determines the padding number. From that, the number of k is known, thus, the state of each 2x2 matrix, that is the number of times each matrix has been rotated one-quarter turn clockwise, can be determined. For each block j of ciphertext characters, each 2x2 matrix will be set to the appropriate state with respect to matrix-value positions and reverse the rotation direction to counterclockwise for each block j.
. The ciphertext length, len, is known which also determines the padding number. From that, the number of k is known, thus, the state of each 2x2 matrix, that is the number of times each matrix has been rotated one-quarter turn clockwise, can be determined. For each block j of ciphertext characters, each 2x2 matrix will be set to the appropriate state with respect to matrix-value positions and reverse the rotation direction to counterclockwise for each block j. Object | Dimension | Number Required |
|---|---|---|
Pseudo-Key XOR Row Vector | 1x4 | 12 |
Pseudo-Key XOR Row Vector | 1x8 | 2 |
Pseudo-Key XOR Row Vector | 1x16 | 3 |
Key Matrix | 4x4 | 8 |
Key Matrix | 8x8 | 4 |
Key Matrix | 8x8 | 1 |
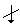 symbol. Normally the down-arrow represents an input and the number of bits (to the right of the forward slash /). And again, traditionally the Hill Cipher literature nearly always represents alphabet characters as both input and output, rather than a number of bits. Following this tradition, and in slight abuse of the bit-use in conventional encryption-decryption diagrams, the number represented in Figure 5 in the upper right of the forward slash / will represent the number of alphabet characters that will input in the direction of the down-arrows rather than the number of bits.
symbol. Normally the down-arrow represents an input and the number of bits (to the right of the forward slash /). And again, traditionally the Hill Cipher literature nearly always represents alphabet characters as both input and output, rather than a number of bits. Following this tradition, and in slight abuse of the bit-use in conventional encryption-decryption diagrams, the number represented in Figure 5 in the upper right of the forward slash / will represent the number of alphabet characters that will input in the direction of the down-arrows rather than the number of bits. 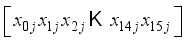 for character
for character 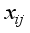 where i is the character number and j is the block number.
where i is the character number and j is the block number. 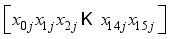 XOR
XOR 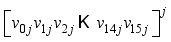 modulo p, where
modulo p, where 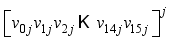 is interpreted as
is interpreted as 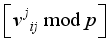 for i = 0 to 15.
for i = 0 to 15. 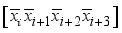 , in Figure 5 to xor in step 4.
, in Figure 5 to xor in step 4. 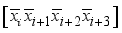 in the above step with the jth power each of one of the 4 random 1x4 pseudo-key xor row vectors respectively.
in the above step with the jth power each of one of the 4 random 1x4 pseudo-key xor row vectors respectively. 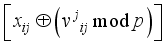 for i = 0, 3 in Figure 5 remembering these computations are preformed modulo p for prime p.
for i = 0, 3 in Figure 5 remembering these computations are preformed modulo p for prime p. 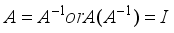 where I is the identity matrix, and by inspection that the matrix is not circulant.
where I is the identity matrix, and by inspection that the matrix is not circulant. 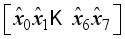 and
and 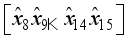 .
. 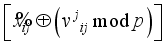 for i = 0, 1 in Figure 5 ensuring all computations are completed modulo p for prime p.
for i = 0, 1 in Figure 5 ensuring all computations are completed modulo p for prime p. 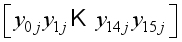 representing the jth block of plaintext
representing the jth block of plaintext 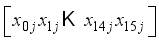 .
. Modulus | nxn Matrix | Number of Possible Permutations in Matrix slots |
|---|---|---|
26 | 2x2 Matrix | 264=456,976 |
29 | 2x2 Matrix | 294=707,281 |
191 | 2x2 Matrix | 1914=1,330,863,361 |
191 | 4x4 Matrix | 1916>3.137E36 |
191 | 8x8 Matrix | 19164>9.685E145 |
191 | 16x16 Matrix | 191256>8.801E583 |
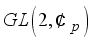 : the General Linear Group of invertible 2x2 matrices over the integers
: the General Linear Group of invertible 2x2 matrices over the integers 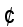 modulo prime p
modulo prime p 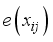 can be created which avoids the control characters with
can be created which avoids the control characters with 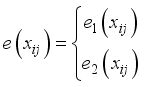 . Even though a message may only be defined to say the English alphabet, ISO 8851-1 allows greater semantic clarity and disambiguation.
. Even though a message may only be defined to say the English alphabet, ISO 8851-1 allows greater semantic clarity and disambiguation. Modulo p | |
|---|---|
26 | 157,248 |
29 | 682,080 |
191 | 1,323,859,200 |
jth Block of the ith Matrix of order n | |
jth Block of the ith Character Raised to the jth Power | |
XOR | Exclusive-or Function |
General Linear Group of degree 2 (2x2) Invertible Matrices Over the Integers, |
| [1] | Hill, L. S. Cryptography in an Algebraic Alphabet. The American Mathematical Monthly. 1929. 36(6), 306-312. |
| [2] | Hill, L. S. Concerning Certain Linear Transformation Apparatus of Cryptography. The American Mathematical Monthly. 1931, 38(3), 135-154. |
| [3] | Sharma, N., Chirgaiya, S. A Review of Modern Hill Cipher Techniques. International Journal for Scientific Research & Development. 2013, 1(10), 2198-2202. |
| [4] | Agrawal K., Gera A. Elliptic Curve Cryptography with Hill Cipher Generation for Secure Text Cryptosystem. International journal of computer applications. 2014 Jan 1, 106(1). |
| [5] | Dawahdeh Z. E., Yaakob S. N., bin Othman R. R. A New Image Encryption Technique Combining Elliptic Curve Cryptosystem with Hill Cipher. Journal of King Saud University-Computer and Information Sciences. 2018 Jul 1, 30(3), 349-55. |
| [6] | Santoso YS. Message Security Using a Combination of Hill Cipher and RSA Algorithms. Jurnal Matematika Dan Ilmu Pengetahuan Alam LLDikti Wilayah 1 (JUMPA). 2021 Mar 30, 1(1), 20-8. |
| [7] | Arifin S., Kurniadi F. I., Yudistira. I. G., Nariswari R., Murnaka N. P., Muktyas I. B. Image Encryption Algorithm Through Hill Cipher, Shift 128 Cipher, and Logistic Map Using Python. In 2022 3rd International Conference on Artificial Intelligence and Data Sciences (AiDAS) 2022 Sep 7, 221-226. |
| [8] | Wen H, Lin Y, Yang L, Chen R. Cryptanalysis of an Image Encryption Scheme using Variant Hill cipher and Chaos. Expert Systems with Applications. 2024, Sep 15, 250, 123748. |
| [9] | Hasoun R. K., Khlebus S. F., Tayyeh H. K. A New Approach of Classical Hill Cipher in Public Key Cryptography. International Journal of Nonlinear Analysis and Applications. 2021 Nov 1, 12(2), 1071-82. |
| [10] | Levine J, Nahikian HM. On the Construction of Involutory Matrices. The American Mathematical Monthly. 1962 Apr 1, 69(4), 267-72. |
| [11] | Achary, B., Jena D., Patra S. K, Panda G. Invertilbe, Involutory and Permutation Matrix Generation Methods for Hill Cipher System. International Conference on Advanced Computer Control, Singapore, Singapore, 2009; 410-414. |
| [12] | Putera A, Siahaan U, Rahim R. Dynamic Key Matrix of Hill Cipher Using Genetic Algorithm. Int. J. Secur. Its Appl. 2016 Aug 1, 10(8), 173-80. |
| [13] | Reddy KA, Vishnuvardhan B, Krishna AV. A Modified Hill Cipher Based on Circulant Matrices. Procedia Technology. 2012 Jan 1, 4, 114-8. |
| [14] | Coggins III P. E., Glatzer T. An Algorithm for a Matrix-Based Enigma Encoder from a Variation of the Hill Cipher as an Application of 2× 2 Matrices. Primus. 2020 Jan 2, 30(1), 1-8. |
| [15] | Santoso H, Rambe NS, Suhardi S. Combined Performance of Hill Cipher and Rivest Code 6 (Rc6) Algorithms in Image Security. IJISTECH (International Journal of Information System and Technology). 2024 Apr 30, 7(6), 379-85. Akreditasi No. 158/E/KPT/2021. |
| [16] | Hassan A., Garko A., Sani S., Abdullahi U., Sahalu S. Combined Techniques of Hill Cipher and Transposition Cipher. Journal of Mathematical Letters. 2023, 1(1), 57-64. |
| [17] | ElHabshy, A. A. Augmented Hill Cipher. International Journal of Network Security. Sept 2019, 21(5), 812-818. |
| [18] | Rekha G., Srinivas V. A Novel Approach in Hill Cipher Cryptography. 2023, 11(6), 3503-3505. |
| [19] | Khalaf AA, Abd El-karim MS, Hamed HF. A Triple Hill Cipher Algorithm Proposed to Increase the Security of Encrypted Binary Data and its Implementation Using FPGA. In2016 18th International Conference on Advanced Communication Technology (ICACT) 2016 Jan 31, 752-759. |
| [20] | Sastry, V. U. K., Samson Ch. A Generalized Hill Cipher Involving Different Powers of a Key, Mixing and Substitution. International Journal of Advanced Research in Computer Science. July-August 2012, 3(4), 191-197. doi unavailable |
| [21] | Shannon, C. E. Communication Theory of Secrecy Systems. Bell Systems Technical Journal. 1949, 28(4), 656-715. |
| [22] | Hodges, J. H. The Matrix Equation X2 – I = 0 Over a Finite Field. The American Mathematical Monthly. Aug. – Sep., 1958, 65(7), 518-520. |
| [23] | Overbey, J., Traves, W., & Wojdylo, J. (2005). On The Keyspace Of The Hill Cipher. Cryptologia, 29(1), 59–72. |
APA Style
Coggins, P. E. (2024). Two Novel Multidimensional Affine Variations of the Hill Cipher. Mathematics and Computer Science, 9(3), 46-56. https://doi.org/10.11648/j.mcs.20240903.11
ACS Style
Coggins, P. E. Two Novel Multidimensional Affine Variations of the Hill Cipher. Math. Comput. Sci. 2024, 9(3), 46-56. doi: 10.11648/j.mcs.20240903.11
AMA Style
Coggins PE. Two Novel Multidimensional Affine Variations of the Hill Cipher. Math Comput Sci. 2024;9(3):46-56. doi: 10.11648/j.mcs.20240903.11
@article{10.11648/j.mcs.20240903.11,
author = {Porter Eldridge Coggins},
title = {Two Novel Multidimensional Affine Variations of the Hill Cipher
},
journal = {Mathematics and Computer Science},
volume = {9},
number = {3},
pages = {46-56},
doi = {10.11648/j.mcs.20240903.11},
url = {https://doi.org/10.11648/j.mcs.20240903.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.mcs.20240903.11},
abstract = {Two novel symmetric multidimensional affine nested variations of the Hill Cipher are presented. The Hill Cipher is a block polygraphic substitution encryption scheme based on a linear transformation of plaintext characters into ciphertext characters. In the time since Hill first published his encryption scheme, variations, modifications, and improvements of theoretical and practical importance have been published every year indicating that the Hill Cipher is an active area of cryptography research. The first variation presented in this paper incorporated invertible key matrices of orders 2, 4, and 8 such that the matrix values of the 2×2 matrix rotate positions with each block of characters in a similar manner to the rotating letter wheels of a German Enigma Encoder, then results of the 2×2 key matrices output are passed to 4×4 key matrices, and 8x8 key matrix, 4×4 key matrices, and rotative-value 2×2 key matrices. The second variation is configured with invertible key matrices of orders 4, 8, and 16 without rotation of matrix values in a similar manner to the first variation. In both variations, plaintext characters of each block are operated on by exclusive-or (XOR) vectors prior to multiplication with the matrices to create the affine ciphers. Strengths, weaknesses, and other considerations are provided in the discussion. Two proposals are also argued with rationale for a more robust character set for encryption and the increase in modulus that the character set allows, and the possible advantages and disadvantages of affine XOR vectors.
},
year = {2024}
}
TY - JOUR T1 - Two Novel Multidimensional Affine Variations of the Hill Cipher AU - Porter Eldridge Coggins Y1 - 2024/07/23 PY - 2024 N1 - https://doi.org/10.11648/j.mcs.20240903.11 DO - 10.11648/j.mcs.20240903.11 T2 - Mathematics and Computer Science JF - Mathematics and Computer Science JO - Mathematics and Computer Science SP - 46 EP - 56 PB - Science Publishing Group SN - 2575-6028 UR - https://doi.org/10.11648/j.mcs.20240903.11 AB - Two novel symmetric multidimensional affine nested variations of the Hill Cipher are presented. The Hill Cipher is a block polygraphic substitution encryption scheme based on a linear transformation of plaintext characters into ciphertext characters. In the time since Hill first published his encryption scheme, variations, modifications, and improvements of theoretical and practical importance have been published every year indicating that the Hill Cipher is an active area of cryptography research. The first variation presented in this paper incorporated invertible key matrices of orders 2, 4, and 8 such that the matrix values of the 2×2 matrix rotate positions with each block of characters in a similar manner to the rotating letter wheels of a German Enigma Encoder, then results of the 2×2 key matrices output are passed to 4×4 key matrices, and 8x8 key matrix, 4×4 key matrices, and rotative-value 2×2 key matrices. The second variation is configured with invertible key matrices of orders 4, 8, and 16 without rotation of matrix values in a similar manner to the first variation. In both variations, plaintext characters of each block are operated on by exclusive-or (XOR) vectors prior to multiplication with the matrices to create the affine ciphers. Strengths, weaknesses, and other considerations are provided in the discussion. Two proposals are also argued with rationale for a more robust character set for encryption and the increase in modulus that the character set allows, and the possible advantages and disadvantages of affine XOR vectors. VL - 9 IS - 3 ER -